Basic Category Theory for Programmers, Part 5: Monoidal Categories
"Monoids are everywhere!" – Bartosz Milewski1
Previous: Basic Abstract Algebra
In the previous post we discussed different kinds of monoids which are commonly found in programming languages. These include Number, Array and String. We also discussed how every object in a category is a monoid where the elements are arrows and the operation is composition. A monoid in this sense "adds" arrows through composition. But how can we express the properties of monoid objects, such as Number, Array and String, in category theory?
There is a fundamental problem we have to deal with. A monoid's operation is binary. It takes two elements and returns a single element. But the arrows in a category go from a single object to another. We need a way to represent the pair of elements which are the arguments of the monoidal operation. Looking at this from a programming perspective, we can start by putting the two elements in a tuple. For example, the two arguments for a binary Number operation could be represented with the tuple, (Number,Number). We can now have a function which takes the tuple as a single argument, performs an operation and returns a Number. This function can now be represented with an arrow in a category.
In PL, our programming language considered as a category, Number and the tuple (Number,Number) are just two objects among many others. To focus in on these objects, we can isolate them into separate categories. Each category will have a single object. One will contain (Number,Number) and the other will contain Number. We will then represent the monoidal operation as an arrow between these two categories. You will notice that since we are going from one category to another, we are dealing with a functor.
The tuple category is a product category. A product category consists of pairs of objects from two other categories. For two categories A and B, the product category is composed of all the pairs (A,B). With a little math background you could see that this corresponds to the Cartesian product of two sets. In our current discussion, both categories are the Number category and the elements of the product category are the pairs (Number,Number). To be more specific, this tuple category contains all the tuples consisting of a combination of two Numbers, (1,1), (1,2), (1,3), (2,1), (2,2), etc.
We are representing the elements of a product category with a tuple, (A,B). This is helpful for understanding how these ideas relate to programming. In the context of mathematics, the product element is usually represented with the symbol "×", A×B. This symbol looks like the multiplication symbol and it matches the idea that this is a "product" category. But keep in mind that it doesn't necessarily mean the two elements will be used in multiplication.
We are starting to see that to represent a monoid in a category we need a special category that is equipped with specific arrows. This category is called a monoidal category. It provides a context where we can identify the monoidal properties of some object in this category. A monoidal category, C, requires a functor from C×C to C. This functor is called the monoidal product and is represented with the symbol ⊗.
We can think of this functor as performing an operation on two values and returning a single value. But keep in mind that a functor is actually a mapping between two categories. In this case, every tuple of Numbers in the product category is mapped to a single value in the Number category.
A monoidal category provides the context for a monoid, but not every object in this category is necessarily a monoid. Also, the monoidal product may not necessarily satisfy all the requirements for a monoid. We have to be more specific. We'll call the monoid object M. The monoid operation is called multiplication and is represented with the Greek letter "mu".
Rememeber that a monoid structure has three parts, a set of elements, an operation, and an identity object. The identity element must be some element in C. We'll call it I. But we can't deal with elements directly in category theory, so we need to express it as an arrow. This arrow is called unit and is represented with the Greek letter "eta".
We can think of it as an arrow which picks the identity element out of C.
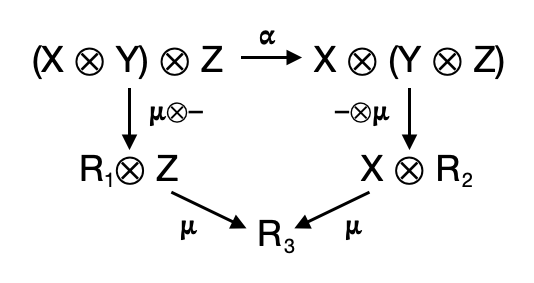
We now have the basic parts for a monoid, but we still need to express associativity and the properties of the identity element. The first is accomplished with an arrow called associator. It is represented with the Greek letter "alpha".
The arrow works on three elements in C, which we're calling X, Y, and Z. The first thing to notice is that this arrow goes in both directions. It is really two arrows where one is the inverse of the other. We mentioned that arrows are also called morphisms. An arrow with an inverse such as this is called an isomorphism. This establishes a sort of equality between the two sides of the arrows. It doesn't say that the two sides are the same thing, but we can map back and forth between them.
Now we can apply monoidal multiplication to the different parts of the associator equation. We'll use R for the result of multiplication.
If X, Y and Z are instances of the monoid M, we should get the same result for both series of operations. We can show this as a commutative diagram.
We can now turn to the identity requirements. A monoidal category requires two more isomorphisms called the left unitor and the right unitor. They are represented by the Greek letters "lambda" and "rho".
This says that the monoidal product of I and some element A is isomorphic with A. This sort of looks like monoidal multiplication with the unit element, but we don't know that yet. These are only isomorphisms that allow us to go back and forth between the different elements.
When we performed operations on Numbers it was easy to see what the result should be if one of the elements was the identity element. But we need a way to express this idea at a more general level where the results of monoidal operations may be harder to understand. In defining the left and right unitor we used A to represent an element because we didn't know if it was a monoid object. Let's assume it is now.
This is where 𝜂 helps us take the next step. 𝜂 goes from I to M. We can apply it to the I in the left hand sides of 𝜆 and 𝝆. After doing that we can apply 𝛍.
Now we have a way of demonstrating the identity rules using arrows. A monoid requires that the following two diagrams commute.
We can now express the monoidal character of an object using category theory. We can take any of our regular monoids, such as Number, Array and String and see how it applies to them. For example we can take a couple of elements of Array, [1,2,3] and [4,5]. In the product category they would look like this, ([1,2,3],[4,5]). Using the Array’s append operation we could do this.
We won't show how all the different arrows and rules apply. It should be easy to see for our simple monoids.
We have taken the concepts for an algebraic structure and translated them into category theory. This process is called categorification. This allows category theory to go down one level and look at simpler structures through the theory. But we can now also take the monoid concept and go up to a higher level of category theory. We'll do this in the next and final post.