Basic Category Theory for Programmers, Part 3: Functors
In the first post of this series we saw that there is a relationship between Array and PL, the category representing our programming language. In category theory, a functor is a mapping between categories. It matches the objects and arrows in one category with the objects and arrows in another. We seem to have a functor between Array and PL. But not all mappings are functors, a functor must satisfy specific requirements.
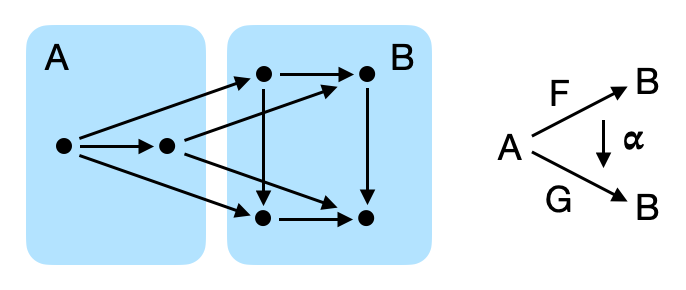
Suppose we have two categories, A and B. Category A has two objects, x and y, and category B has its own two objects, m and n. There is an arrow from x to y called f, and another arrow from m to n called g.
Now suppose we have a functor which maps x to m, y to n, and f to g.
Notice that there are two paths from x to n.
A set of objects and arrows is called a diagram. A diagram is commutative when the different paths which start at one object end up at the same object and both paths lead to the same result. The diagram we sketched above is commutative between x and n if, for every x, following both paths give us the same result for n.
We can also express commutativity in terms of arrow composition. Let's say xm is the arrow from x to m and yn is the arrow from y to n. Then we can say that our diagram is commutative if the following is true.
Let's see what this looks like in PL. A represents our main category, PL, and B can be any type that can act as a functor. For now let's take Array as the category B. Then let's focus on a couple of objects in A, the types Number and String in PL.
The arrow between Number and String represents all the functions between Number and String and it corresponds to the arrow f in the diagram above. To have a functor, we need to map the objects and arrows in A to objects and arrows in B.
The arrows that go from objects in PL to objects in Array correspond to Array constructors or initializers. The arrow from Number to Array<Number> is the constructor which takes a Number and returns an Array with that Number. Similarly for the arrow from String to Array<String>.
All we need now is to map f. We need a function that goes from Array<Number> to Array<String> corresponding to the arrow g in our initial diagram. We can use the Array function which is typically called map. It is a higher-order function which takes another function as its argument. The argument function converts a Number to a String. The map function then applies the given function to each element of the Array.
We now have a mapping between objects and arrows, but we still need to check for commutativity. Let's use specific values to make this clear. If we pass the Number 3 to the toString function we get "three". If we pass the 3 to the Array constructor, we get [3]. If we pass "three" to the Array constructor we get ["three"]. If we pass toString to the map function on [3], we also get ["three"]. We got the same answer no matter what path we took. This isn't a rigorous mathematical proof, but it looks like Array with the map function behaves as a functor.
Diagrams of functors show two categories and the mappings between them. But we shouldn't think of a functor as a set of two categories. A functor is the mapping between the categories. We can think of it as the set of all the mappings of objects and arrows between the two categories.
Let's see if we can find another functor in PL. Suppose we have a function named toNumber which takes a String and returns a Number. For the String "3" it will return the Number 3. But how are we going to handle Strings that don't represent valid Numbers? One approach is to use a type which works as a container. If we can generate a Number, we will return that Number in the container. If we can't generate a Number we will return an empty container. We'll call this type Optional, but other names for it include Maybe, Option, and Nullable.
The Optional type is usually an enumeration with two cases. One case represents the empty state and the other case holds an actual value. The empty case is often called none or empty. We used angle brackets to show that an Array can hold different types. The Optional type can also hold different types so we can use the same convention here. An Optional that can hold a String would be Optional<String>.
Like Array, Optional has a map function which allows us to convert an Optional of one type into an Optional of another type or to transform its value in some way. We can show that the various functions for Optional also form a commutative diagram. From "3" we can construct Optional("3"). From 3 we can construct Optional(3). The toNumber function goes from "3" to 3, and if we pass this function to the Optional map function on the Optional("3") value, it returns Optional(3). This shows, very loosely, that Optional with the map function is also a functor.
Note that these two functors behave differently. An Array may hold multiple values of some type. When we apply a function using map, that function is used to transform all the values in the Array. With Optional, the map function is only applied to one value if the Optional happens to hold one. If the Optional holds a none case the map function does nothing. Both functors preserve the structure of PL, but they do it in a totally different manner.
Now let's look at one more type. Some programming languages have a Result type which is used to represent the result of an operation that may fail. Like Optional, the Result type is an enumeration, but instead of a none case, it has a case which holds an Error type for situations when the operation fails. Some languages use a type called Either for this purpose. Either is used to hold two types of values, so it is a more general case of Result. The Result type is constrained in that one of its cases must hold some kind of error.
Result is a little different from Array and Optional because it may have two different map functions, one which works on the success value and another which works on the error value. The map functions are similar to the one in Optional in that they each work on one case and ignore the other. We won't go over the details but we can see that based on the analysis of Optional, Result should also also be a functor. In fact it can be a functor in two different ways since we can map on the success type as well as on the error type. A functor which maps two categories is called a bifunctor.
We have to make an important clarification. We are saying that Array and Optional are functors, but as we mentioned above, a functor is a mapping between categories. We are actually using the term "Array" in three different ways. In one sense, Array is an object in PL. In another sense, Array is a category. The Array category is composed of Array objects! Then we said that Array is a functor. When used in this sense, we have to keep in mind that we are talking about the mapping between PL and Array (the category). We could use more technical terms to differentiate these different senses, but the meaning is generally obvious from the context.
A functor is a mapping between categories. But we can also have mappings between functors. These are called natural transformations. Given two categories, A and B, and two functors F and G, which both go from A to B, a natural transformation from F to G maps the objects and arrows in F to the objects and arrows in G. The mapping from F to G should also form a commutative diagram similar to what we described for functors.
This may sound complicated, but programming languages are actually full of natural transformations. Let's look at a simple natural transformation between Array and Optional. An Array typically has a function called first which returns the first element of the Array. But what if the Array is empty? We could require that a programmer must check that an Array is not empty before calling first. And if the programmer insists on calling first on an empty Array we crash the program.
We can take a better route to solve this problem. Instead of crashing, the first function could return an Optional value. We then return the first value if it is available, and we return Optional(none) if the Array is empty. This function represents a natural transformation since it is going from one functor to another, and both functors originate in the same category. We didn't check the commutative diagram, but let's assume it checks out for now. The target category would consist of all the functor types which satisfy the requirements for natural transformations, allowing us to map between the different functors.
Natural transformations are everywhere. It seems like we have only given a fancy name and a complicated description for familiar functions. But there is a more interesting way to map between functors. We can generally nest functors of the same type. For example, we can make Arrays of Arrays or Optionals of Optionals. We can do this because these functors contain a type in PL and all the functors are also types in PL.
Let's see how this works. The first function for Array<String> returns an Optional<String>. Now suppose that we want to convert the String to a Number. We could use the map function to convert the Optional<String> to an Optional<Number>. We can’t use the function String→Number because not all Strings are valid Numbers. Instead, we need a function which returns an Optional<Number>. This sounds like the toNumber function which we described above.
The Optional map function is a higher-order function that takes a function A→B. If we start with an Optional<A> it will return an Optional<B>. We can try to use the toString function for A→B, but we have a problem. Let's look at the signature of toString.
String corresponds to the A part, and Optional<Number> corresponds to the B part. This means that the Optional map function will look like this.
We end up with a nested functor! This isn't what we were looking for. We only need one layer of Optionals. But we're in luck because many programming languages have a function called flatMap which will "flatten" the Optional for us. If we use the toString function with flatMap, it will give us the result we are looking for.
This is convenient, but what is going on? The map function is related to functors. It simply transforms the values contained in the functor. But flatMap is doing some magic behind the scenes. To understand what's going on from a category theory perspective we need a little more math. The next post will give a quick overview of abstract algebra. This will give us the tools we need to explore another set of important concepts in the final two posts in this series.



Really great stuff.
Upon reading I found that the map function may be confusing. Based on the diagram you might think map is a function that takes an Array<Number> and turns it into an Array<String>. This is true in programming languages that provide a method called map on the functor type. But there is a method map and there is also a free function map that is unique to each functor. The free function map would take as input toString and have as output the function between Array<Number> to Array<String>.